Have you ever had a discussion with your child about why they need to be able to do math when “Nowadays we have technology and everyone just uses a calculator”? I mean (eye roll and sigh)… Who is this “everyone”, anyways? Kids are great at making you feel out of the loop and old at the same time, aren’t they?
In my house, it’s more commonly the “Why do I need to care about spelling when autocorrect will just fix my mistakes?” argument.
“Because the computer may no the correct spelling butt it doesn’t always no how two judge the context. That’s why!” Anyways, I digress… Numbers. We were talking about numbers.
Numbers matter.
As much as I grumbled my way through math class, numbers actually turn out to be hugely important. In the vaccine discussion, numbers help us look at the rates of infection, the incidence of disease, the relative risk of illness in a vaccinated vs unvaccinated population, and so on. But this is not a statistics lesson.
In this blogpost, I want to focus on how we look at numbers and how the meaning we attribute to those numbers can change the way we think about the risk of disease and the benefit of vaccines. We will use two examples to illustrate this fact. The first example will look at the deaths from influenza in the United States during the 2017-18 flu season. The second example will look at graphical representations of numbers and how the scales being used can make vaccines look more or less impactful.
Example #1: US flu deaths during the 2017-18 flu season
• The CDC lists the average number of US deaths from influenza as ranging from 12,000-56,000, depending on the year. In 2017-18, over 80,000 people died from the flu. 186 of these were children. That’s a huge number. At least it seems so to me. But in discussing this with patients, I have had some say that 80,000 is “not that many”. Knowing that the population of the United States in 2017 was around 325.7 million people, 80,000 could seem like a drop in the bucket.
But let’s break this down and look at these numbers in different ways to get a sense of how our interpretation of, or feelings about, numbers can change our view.
Image adapted from PsychologyToday.com
• Let’s ask ourselves how we feel about the following numbers. Which report seems worse?
o 80,000 people in the US died of the flu in 2017-18
o 0.024% of people in the US died of the flu in 2017-18
o 1 out of every 4071 people in the US died of the flu in 2017-18
If I didn’t already know that all of these numbers are the same, representing the exact same number of deaths (Yep, it’s true), I would likely feel that one in every 4071 people in the US dying was a very big number, much worse than the others. While 80,000 out of 325.7 million doesn’t seem as bad and 0.024% of the population seems pretty small. What did you think about these numbers?
• What if we were to say it in a way that seems more real to us? For example, what if we read the headline:
o “The entire sold out crowd at the New York Giants’ Met Life Stadium died of the flu yesterday.” Or…
o “Eighty thousand people died when 152 Boeing 747 jetliners crashed, killing everyone on board. The cause? Influenza.”
Somehow, thinking about an entire football stadium of people dying of an illness seems more impactful. Is that because the loss of life all at once seems worse than a one-by-one loss over the year? It’s still 80,000 lives lost. 80,000 loved ones gone.
And the 152 jetliners crashing feels much scarier – perhaps because many of us have a fear of dying in a plane crash at baseline. Whereas, the flu is often thought of as “no big deal” and is not nearly as frightening. Still, 80,000 people dead is 80,000 people dead, no matter how they died.
Example #2: A graphical representation of measles data
• Let’s look at the two graphs shown below. They both depict deaths from measles. The first (Graph A) is used to demonstrate the significant impact that introduction of the measles vaccine made in decreasing illness and reducing loss of life from this deadly disease.
The other (Graph B) is used by anti-vaccine proponents to suggest that there was little impact of introduction of the vaccine on reduction in deaths and that that reduction had already begun before vaccine became available. The funny thing is that these two graphs, seemingly showing opposite findings, are using the exact same numbers. How those numbers are represented makes a big difference. Let’s dig in…
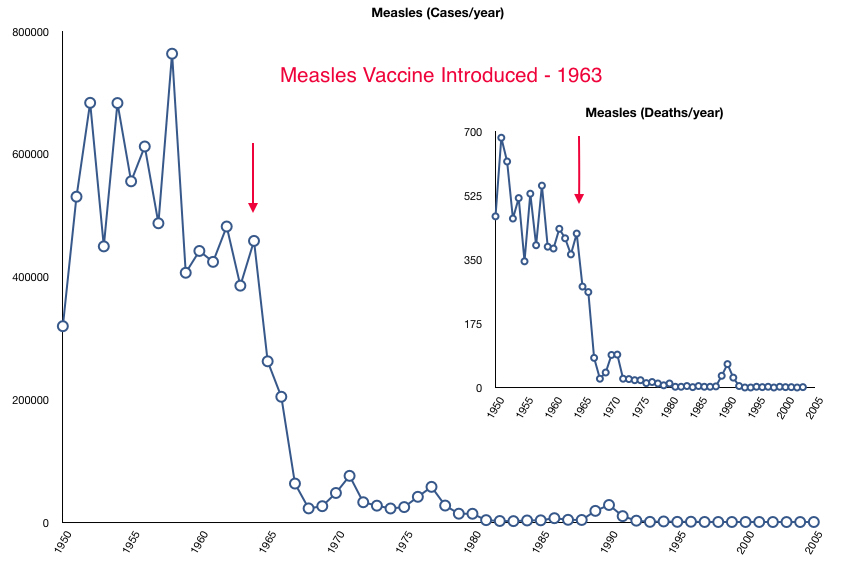
Graph A: The larger graph above shows cases per year before and after introduction of the measles vaccine in 1963 (red arrows). The smaller, inset graph shows the # of deaths per year before and after the vaccine. After the vaccine, we see quite a precipitous drop in both cases (from around 450,000 cases before vaccine to fewer than 1000 after) and in deaths (from around 450 to near zero).
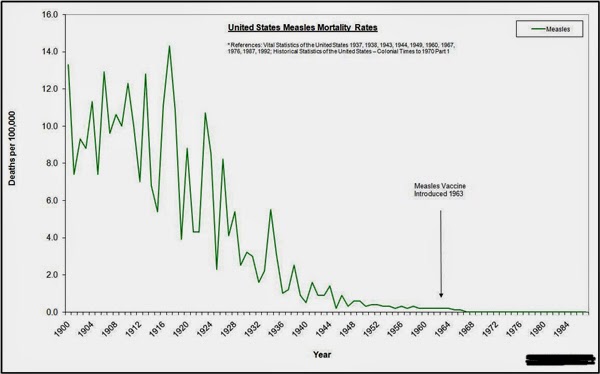
Graph B: Taken from an anti-vaccine website, this graph also looks at measles mortality (death) rate over the years, both pre and post introduction of the measles vaccine (black arrow). According to this graph, the impact of the vaccine doesn’t look that impressive, does it?
Break out your paper and pencil. Let’s do the math!
• In order to properly interpret what is being presented here, we have to do some math. The vertical axis lists deaths per 100,000 people. Let’s look at the same timeframe as discussed in Graph A, just before the vaccine was introduced in 1963. On this graph, it is difficult to estimate but, for argument’s sake, let’s say that there was 0.25 deaths per 100,000 people in 1962.
Now we need to know how many people lived in the US in 1962. Census data tells us that there were 186.5 million people at that time. 186.5 million divided by 100,000 is 1,865. If we multiply that by 0.25, we get 466 people that died from measles that year. This is approximately the same number as we got using the estimated number of deaths from Graph A. The CDC actually recorded 481,530 cases of measles and 408 deaths in 1962, so our estimates are fairly accurate.
• Both graphs show the same number of deaths but the use of deaths per 100,000 people makes that number seem much less impressive. Unless we do the math (which I’m guessing many people don’t do), we would assume from looking at Graph B that the introduction of the measles vaccine in 1963 really didn’t make much of a difference.
• Of course, mortality from measles is not the only thing that bears looking at. We know that morbidity (brain swelling, pneumonia, seizures, hospitalizations, etc.) from measles is significant. If we look at the actual number of cases of disease as seen in Graph A we can easily see that the vaccine markedly decreased morbidity and mortality from measles.
Emotion before reason? Let’s pause and dig deeper.
We respond to data in much the same way that we respond to events in our lives – emotion comes before reason. Evolutionarily speaking, this more rapid emotional response is important. If an enemy is bearing down on us, our fight or flight response – fear – needs to kick in so that we can run away and save ourselves. Only after we escape will we more fully analyze the threat. But when it comes to numbers and data, emotional reactions (and first impressions) can sometimes lead us astray.
We owe it to ourselves, to our loved ones, and to our communities to dig a bit deeper into the information that we are being shown about vaccines. And when we do, we will find that the numbers say the same thing every time. They tell us that vaccine-preventable diseases are deadly and that vaccines work. Vaccines save lives!
So, go ahead. Do the math. You can even use your calculator – I promise I won’t tell.

How many lives does the flu vaciine save?
Here’s an article looking at this question: the short answer, about 40,000 over 9 years just in the US. https://www.sciencedirect.com/science/article/pii/S0264410X15002315
But don’t forget, the flu also causes hundreds of thousands of hospitalizations and millions of people get sick – that is a huge financial burden each year on society. Here’s an article looking at illness and hospitalization averted by flu vaccination:
https://www.cdc.gov/flu/about/burden-averted/2017-2018.htm
How many are vaccinated for the flu and end up getting the flu.
So, in its best years, the flu vaccine is around 60% effective. This means that around 40% of people who are immunized still get the flu. But what we know from looking back at people who died from the flu is that around 80-90% of them were not vaccinated. So, while the flu vaccine isn’t 100% effective at preventing influenza, it is highly effective at preventing hospitalizations and death from the flu. I think of it like a seat belt. We want to get our flu shot BEFORE we get exposed to the flu just like we want to put on our seat belt BEFORE we get into a car accident. Otherwise, we are leaving ourselves at risk.
How many people are being listed as death from covid19 coronavirus that are actually other coronavirus such as sars, h1n1, swine, and death from other complications such as bronchitis and or respiratory disease and infection.
The current workflow is to test anyone with serious respiratory, cardiac, or other medical issues that require intensive care for COVID19 as well as other known respiratory pathogens. The “respiratory panel” covers influenza, metapneumovirus, and multiple others. COVID19 is its own specific test. The respiratory panel does not include SARS or MERS but there have been no cases of this in the US in the recent past as far as I know. Some have tested positive for both flu and COVID19 but this is rare. If one passes away in the setting of a + COVID19 test, it is presumed that the cause of death is COVID19 complications. If one passes away in the setting of a + flu test that has put them in intensive care, the presumption is that they died from complications of the flu. Hopefully that makes sense.
What is the death rate of vaccines. How many die from getting the vaccine itself?
The rate of life-threatening reactions (this is not deaths – the rate of death would be significantly lower as many of these conditions are recoverable) is 1-2 in 1 million vaccines. “A 2013 study using electronic health record databases reviewed health information on over 13 million vaccinated persons and compared causes of death in the vaccinated study population to the general US population. The death rate 1 or 2 months following vaccination was lower than that in the general US population, and the causes of death were similar“ [McCarthy NL, Weintraub E, Vellozzi C, Duffy J, Gee J, Donahue JG, et al. Mortality rates and cause-of-death patterns in a vaccinated population. Am J Prev Med. 2013;45(1):91-7.
I couldn’t find a full version of the cited study: Does the study take Socioeconomic Status into consideration in comparing the death rates? The reason I ask is because not only are lower SES children/persons less-likely to be ‘fully’ vaccinated, the correlate of poverty to poor health and higher risk of death due to the lack of access to quality health care is well documented. So, not only are those in a higher SES more likely to be vaccinated, they are also more likely to be able to get the care they need for any illness, therefore lowering the death rate for that cohort by comparison.
Second question: Is the 1-2 life-threatening reactions per 1 million vaccines based on doses or vaccine type? If it is doses, and the current vaccine schedule includes 72 doses, math starts to get dicey. 1 million vaccine doses @ 72 doses per fully vaccinated child, would mean 1-2 incidences per 13,889 fully vaccinated children (1 per ~6,900 on the high end). And again, it is important to consider non-life-threatening reactions that are significant (seizures, neurological disorders, paralysis, allergies, etc. where correlative data is hard to come by).
It seems that a definitive stance on vaccination across the board, and a one-size-fits-all approach to vaccination/preventative health care is not justified.
Hey Ryan,
Unfortunately, this article has to be purchased for full access. I honestly don’t recall if I had temporary access prior but I don’t seem to now. I don’t suspect that SES was included given the description below – at least they didn’t list it as one of the variables looked at.
“ Analyses were conducted in 2012. Mortality rates were calculated at 0–1 day, 0–7 days, 0–30 days, and 0–60 days following vaccination for deaths occurring between January 1, 2005, and December 31, 2008. Analyses were stratified by age and gender. Causes of death were examined, and findings were compared to National Center for Health Statistics (NCHS) data.”
This study used the Vaccine Safety Datalink information (see here for details about this dataset: https://www.cdc.gov/vaccinesafety/ensuringsafety/monitoring/vsd/index.html) and compared it to data from the National Center for Health Statistics to see if mortality following vaccination was greater than expected compared to baseline mortality. It wasn’t. And the most common causes of mortality in the vaccinated cases compared to the general population were the same, suggesting no impact of vaccination.
Regarding question #2, here is a good summary for your review (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4599698/#R29). Understanding how the Vaccine Adverse Events Reporting System (VAERS) and the Vaccine Safety Datalink (VSD) work is helpful.
Universal vaccination recommendations always allow for individualization. It is not a one-size-fits all approach. It is a one-size-fits-most approach. And it has to be this way or public health measures don’t work. What if your waiter/waitress wasn’t required to wash their hands after going to the bathroom? Maybe it makes their hands chapped and they don’t like that feeling. Would our rates of food borne illness increase? Yes. What if corporations didn’t have to meet requirements to keep them from dumping harmful chemicals into our water supply because it was inconvenient for them and they would lose money because of it? Our water supply would not be nearly as safe and our population would suffer. Vaccines are no different. We recommend vaccines because they work and because they are generally very safe, but we do take the individual into account. Are you moderately to severely ill? Then you shouldn’t get a vaccine. Are you immune compromised? Then you shouldn’t get a live-attenuated vaccine. Do you have an allergy to a vaccine component or have had a serious reaction to a vaccine in the past? Then you shouldn’t receive that vaccine. And the list goes on. And as far as school mandates go, no one is forcing parents to vaccinate. They always have a choice to home school. People have a right not to vaccinate themselves. But others have a right not to live in fear of contracting a deadly disease from their neighbor or classmate as well.
If you’re in fear of getting it from your neighbor or classmate then you get vaccinated and while at it see what other vaccines are available just in case.
You never know what diseases these people might be carrying.
People who avoid vaccinations lack mathematical comprehension. To be an anti-vaccine activist is to admit mathematical ignorance and scientific ignorance. “My mind is made up; don’t confuse me with facts. (or knowledge)”
I don’t know that they are lacking in mathematical comprehension necessarily but their emotional decision making certainly takes precedence. Accepting something that goes against a strongly held belief is hard for any ego to handle. Sometimes, we ignore facts as a protective mechanism. Getting people to see the equally emotional side of outcomes of illness with vaccine-preventable disease is key. We have to stay open to discussion, stay respectful, and try to get at the root of their fears as fear is often the motivating factor behind the decision to not vaccinate.
What percentage of flu related deaths each year have actually been vaccinated or not for the flu that year? Would be interesting to know, most people tend to think the people that die have not taken the flu shot but I would like to know out of all the deaths what percent was and wasn’t vaccinated.
Good question! Here’s a great site to get more detailed information…
https://www.cdc.gov/flu/about/burden/faq.htm
Short answer, looking back over deaths attributed to flu, typically 80% were unvaccinated.
The 80% pertains to the number of deaths in children, not total population.
Yes, thank you. Flu deaths are reportable in children, meaning we know exactly how many deaths there are, instead of an estimate which is what we have for adults. The 80% figure is based on flu deaths in children and their immunization status for the flu.
If no one in the US got a flu shot, how many people would die from the flu in an average year? We’re at over 350k deaths so far with no Covid shot. Would it be comparable?
That’s a great question. It’s hard to say. The R naught (R0) value (how many other people one person can spread an infection to – it’s contagiousness) is highly dependent on factors outside of the virus itself – how many are vaccinated, hygiene practices, density of the population, etc. The Spanish Flu of 1918 had an R0 value estimated around 1.8 – so one person could spread to almost 2 others. The Spanish Flu (which occurred before a flu shot became available in the 1930s) was much more deadly than we have seen COVID to be (50+ million people died worldwide in one flu season) but this was also before we had the medical and public health advances that we have today. Even with the flu shot (because an unfortunately low number of people tend to get vaccinated – around 30-40% in the young adult population to around 60% in kids/elderly), we saw 80,000+ deaths in 2017-18. With NO vaccine, the rates would undoubtedly be significantly higher, perhaps on the order of what we are seeing with COVID?
Hello! Amazing Article!
I’m doing a high school thesis on the positive effects of Vaccinations, and I wanted to use Graph A as evidence. I was just wondering what website the graph/data came from so I can reference it as well. Thanks!
Hi there! The graph is from my book, Let’s Talk Vaccines: A Clinician’s Guide to Addressing Vaccine Hesitancy and Saving Lives. We edited this graph and had to acquire permission for use (though can’t remember the reference off the top of my head and I don’t have my book handy to look for you). You can google “effects of the measles vaccine on hospitalizations and deaths” and you’ll be able to find similar graphs in “images” – just make sure to reference or get permission for use. Good luck with your thesis!!!